Explaining maths

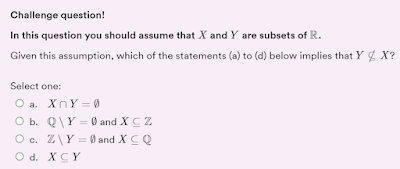
 My fourth FPM quiz last autumn was on sets and subsets. Again the "challenge" question isn't too hard, as long as you understand the basic concepts and definitions, though it is easy to make mistakes. Here is a screenshot of the question. As usual, the buttons don't do anything, but you can enlarge the image by clicking on it. Click on the screenshot to enlarge the image Here \(\mathbb{R}\), \(\mathbb{Q}\) and \(\mathbb{Z}\) have their usual meanings, and \(\emptyset\) is the empty set. You also need to know about the operations of intersection (denoted by \(\cap\)) and set difference (denoted by a backslash, \(\setminus\)) and the "subset" relation (denoted by \(\subseteq\)). Here I use the "subset or equals" notation \(\subseteq\) to make it clear that sets which are equal do count as subsets of each other. In particular, note that the notation \(Y \nsubseteq X\) means that \(Y\) is not a subset of \(X\), which is equivalent to saying tha

My third FPM quiz last autumn was on prime factorization. As usual the final question was labelled as a "challenge question". This one is probably relatively easy once you really understand the definition of the set \(S\), which is closely related to the material from my classes on Bézout's lemma. (But you don't need to know about Bézout's lemma to answer the question.) Here is a screenshot of the question. As usual, the buttons don't do anything, but you can enlarge the image by clicking on it. Note that three of the statements are true and one of the statements is false. You are supposed to spot the false one!

 My second FPM quiz last autumn was a First quiz on rational and irrational numbers . Here is a screenshot of the challenge question. Note added: Thanks for asking about whether zero is a natural number. This varies in the literature, and (as you can check) the answer here depends crucially on this. For my teaching in Nottingham, zero is not included in the natural numbers. So the natural numbers are the strictly positive integers, i.e., \[\mathbb{N}=\{1,2,3,\dots\}\,.\]

Perhaps it would be interesting to post some of my so-called "challenge" questions from my FPM quizzes. I won't post them all at once. Here, as a png image, is the very first "challenge" question I set them, on GCDs (Greatest Common Divisors, also known as Highest Common Factors). It is just a screenshot, so the buttons don't do anything. Enjoy! Screenshot of "challenge" question from FPM First Quiz on GCDs

Last year many of us at the University of Nottingham created Moodle quizzes for our students to practise on. I had some fun with the technical aspects of this, and may post on that another time. Typically my FPM quizzes would have a few relatively routine questions, followed by a "challenge" question (clearly labelled as such) which was intended to stretch them. Quite often we would discuss the challenge questions in the "live" sessions. I also made a small number of "challenge quizzes" (clearly labelled again) where all of the questions were challenge questions. Here is a Piazza post I made to explain one of the "relatively routine" quiz questions related to prime factorization. FPM First quiz on Prime Factorization: question 3 Hi everyone, I have been asked about this quiz question, from the First quiz on Prime Factorization. This is really all about divisibility by primes, and highest powers of primes dividing natural nu

In a first-year FPM workshop last year, I mentioned the diagonal in the Cartesian square of a set, and the connection with reflexive relations on the set. Relations \(R\) on a set \(S\) correspond to subsets \(M\) of \(S\times S\) in a standard way. And then the reflexive relations on \(S\) correspond to those subsets \(M\) of \(S\times S\) such that the diagonal is a subset of \(M\). I had a question on Piazza asking me to explain a bit more about what the diagonal is. Here is my reply.

Here is another question and (incomplete) answer from my Autumn 2020 FPM Piazza Forum. The question under discussion comes from my Sample Exam Paper, and the student was asking how to approach it, and whether the Fundamental Theorem of Arithmetic could help. Here is the question: Question from FPM Sample Exam Paper, Autumn 2020 My (incomplete) answer: I don't want to spoil this completely yet, though the solutions will be available soon! You can (but don't have to) treat the easy special case where \(k=1\) first. Can you do the special cases where \(k=2\) or \(k=10\)? I don't think it does any harm to have the FTA in mind, though it may not help much with the proof. This question involves manipulation of powers of integers, and so I suggest you play around with powers of powers. Best wishes, Dr Feinstein