Connectedness of unions (from this year's MATH4085 Metric and Topological Spaces)

-
In order to formalise the notion of "connected components", we need to know something about when a union of connected sets might be connected. Of course this isn't generally true, e.g. (with the usual topology)

\((0,1) \cup (2,3)\)

is disconnected, but is a union of two connected sets. On the other the union of two disjoint connected sets can sometimes be connected. For example,

\((0,2)=(0,1]\cup(1,2)\)

is connected, even though it is a union of two pairwise disjoint connected sets.
[Can you work out what the true story is here?]

Let's have a look at Lemma 6.12 which gives a sufficient condition for a union of connected sets to be connected. 


Informally, these connected pieces are somehow all "attached" to each other at the point \(x_0.\) The proof of Lemma 6.12 makes this formal.

There are many ways to prove this lemma. For example, we can assume that the union is equal to \(X\) if we like. We can also use a variety of conditions equivalent to connectedness. But here we will work with the union directly and with the definition using clopen sets.

We may assume that \(I\neq \emptyset\), because the empty union is the empty set, which is connected. 

Set

\(\displaystyle X'=\bigcup_{i\in I} E_i\,,\)

and give \(X'\) the subspace topology \(\tau_{X'}\) induced on \(X'\) by the topology on \(X\). Note that \(x_0 \in X'\) (as long as we assume that \(I \neq \emptyset\)).

For each \(i \in I\) we give the set \(E_i\) its subspace topology (from \(X\) or from \(X'\), it doesn't matter), which we denote by \(\tau_i\).
[You might remember that we said in the notes that the subsubspace topology is the same as the subspace topology?]

We know that each \((E_i,\tau_i)\) is a connected topological space.
[For the rest of the proof we work either in the topological space \((X',\tau_{X'})\) or in the topological spaces \(E_i\) with their subspace topologies.]

We have to show that \((X',\tau_{X'})\) is connected.

Let \(A\) be a \(\tau_{X'}\)-clopen subset of \(X'\).
[We show that \(A\) must be either \(\emptyset\) or \(X'\). To detect which, we consider separately the two cases where \(x_0 \in A\) and where \(x_0 \notin A\).]

Case I: Suppose that \(x_0\in A\).

Then, for each \(i \in I\), we have \(x_0 \in A \cap E_i\) and so, in particular, \(A \cap E_i \neq \emptyset\).

But now \((E_i,\tau_i)\) is connected and \(A \cap E_i\) is a non-empty \(\tau_i\)-clopen subset of \(E_i\). By connectedness, we must have \(A \cap E_i=E_i\), i.e., \(E_i \subseteq A.\)

This is true for all \(i\in I\). Thus we have

\(\displaystyle X'=\bigcup_{i\in I} E_i \subseteq A \subseteq X',\)

and so \(A=X'.\)

Case II: Otherwise we have \(x_0 \in X' \setminus A\).

But \(X'\setminus A\) is also a \(\tau_{X'}\)-clopen subset of \(X'.\) So the argument above shows that \(X'\setminus A=X'\), and so \(A=\emptyset\).

Thus the only \(\tau_{X'}\)-clopen subsets of \(X'\) are \(\emptyset\) and \(X'\), as required. \(\quad\square\) 

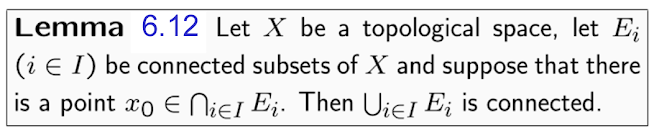
Comments

Post a Comment

Popular posts from this blog

Sums and integration against counting measure: Part I

-
For other posts in this series, see https://explaining-maths.blogspot.com/search?q=Sums+and+integration+against+counting+measure In case the MathJax mathematics below does not display properly in your browser, I have made a PDF of the main article available via my  WordPress blog  at  https://explainingmaths.files.wordpress.com/2023/08/sums-and-integration-against-counting-measure_-part-i.pdf Note added 30/8/23: I'm not quite sure when I started to say "integration against a measure". I'm not alone, but I think that "integration with respect to a measure" is a lot more common! However, I don't want to change the titles of my latest 10 blog posts, so I'll leave it as it is. I'll probably change back to "integration   with respect to a measure" in future though! It has been a while since I wrote a mathematical post! Here I thought I would say something about Measure and Integration which is relevant to my research. For these posts I as
Read more

Discussion of the proof that the uniform norm really is a norm

-
In response to a request on Piazza, I gave a detailed proof that the uniform really is a norm, including some comments and warnings on possible pitfalls along the way. Here (essentially) is what I said. Let’s have a look at \(\|\cdot\|_\infty\) on the bounded, real-valued functions on \([0,1]\) (but you can also work with bounded functions on any non-empty set you like, and the same proof will work). We define \(\ell_\infty([0,1]) = \{f: f \textrm{ is a bounded, real-valued function on }[0,1]\,\}\,,\) and this is the set/space we will look at. So we set \(Y=\ell_\infty([0,1])\). Then you can check for yourselves that \(Y\) really is a vector space over \(\mathbb{R}\) (using the usual "pointwise" operations for functions). Note that the zero element in this vector space is the constant function \(0\) (from \([0,1]\) to \(\mathbb{R}\)), which I'll denote by \(\mathbf{0}\) here for clarity. (We also used \(Z\) for this function in one of the exercises.) I'll first give
Read more

Revisiting liminf and limsup

-
This post is also available in PDF form from my WordPress Blog at  https://explainingmaths.wordpress.com/2023/09/01/revisiting-liminf-and-limsup/ My recent series of posts about Fatou's Lemma for sums was aimed primarily at mathematics students at 3rd-year undergraduate level or above. So I think I should write a post more suitable for first-year undergraduate students. So I'm going to have another look at the topic of $\liminf$ and $\limsup$ for bounded sequences of real numbers (though most of what I say can be generalised to sequences, or even nets, of extended real numbers). I said quite a lot about this in a previous post on my WordPress blog in the post https://explainingmaths.wordpress.com/2009/01/10/an-application-of-absorption-to-teaching-lim-inf-and-lim-sup/ and there was a lot of discussion in the comments below the post. In particular, in those comments, I discussed the $\liminf$ and the $\limsup$ of some examples of sequences $(x_n)$, including the following exam
Read more